青梅煮酒——活跃变量分析

（一）目标

活跃变量分析可以分辨某个变量v的值在程序的p点之后会否再用到。即，是否存在一条路径从点p到结束点，使得变量v的值在v被重定义或者结束之前被用到。

活跃变量分析

（二）对象以及调用过程分析

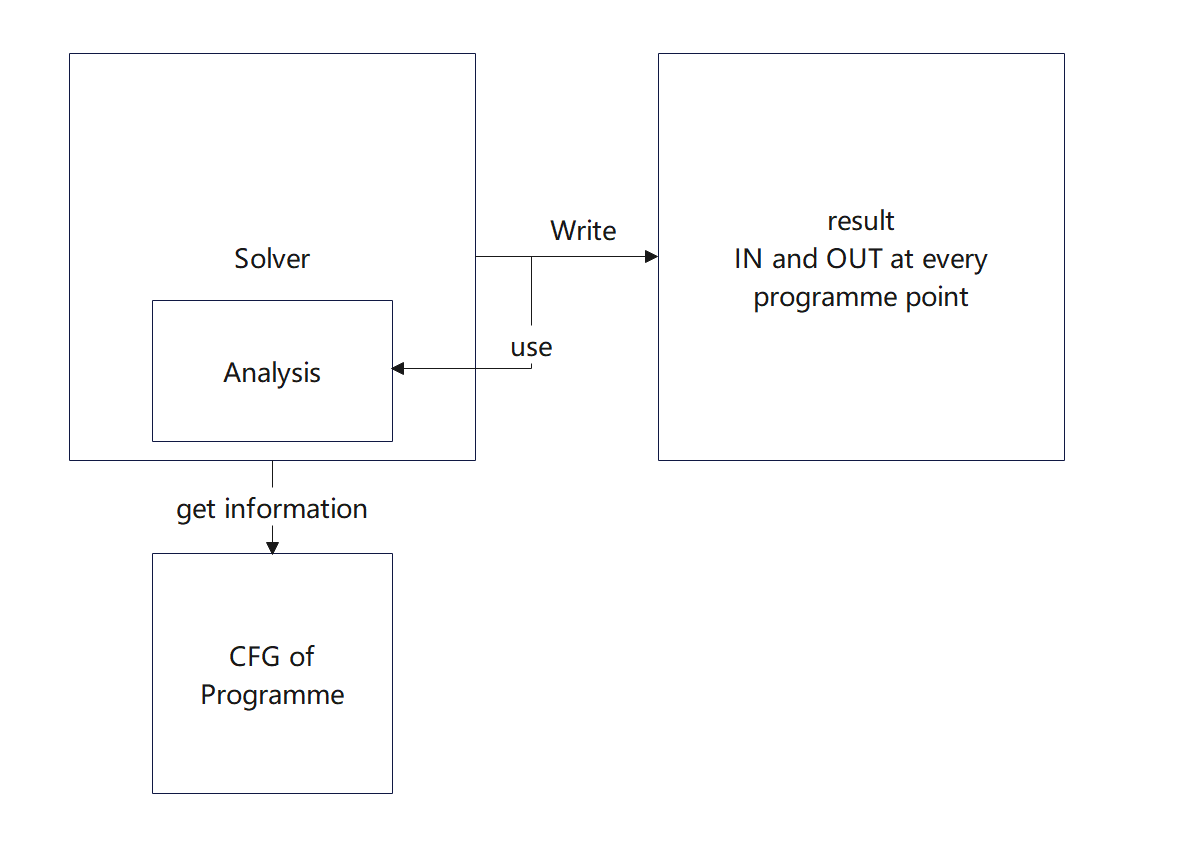
1、Solver->IterativeSolver

Solver是分析器的抽象表示，其中具体做出分析的类型为DataflowAnalysis<Node, Fact>类型，分析器的工作分为两个阶段：初始化和求解。
IterativeSolver是更加具体细节的迭代分析器对象，其中完成了doSolveForward以及doSolveBackward的实现，在doSolveBackward中，我们实现活跃变量分析的代码即可。

2、DataflowResult

在《软件分析》课程讲述的算法中，对于每一个基本块都有一个IN，OUT集合，标示着“我们感兴趣”的静态分析问题的抽象。可以说，一个DataflowResult就是我们分析该问题的结果。

public class DataflowResult<Node, Fact> implements NodeResult<Node, Fact> {
    private final Map<Node, Fact> inFacts = new LinkedHashMap<>();
    private final Map<Node, Fact> outFacts = new LinkedHashMap<>();
    ……
}

3、Analysis

Analysis是本次实验的核心部分，对于不同的分析，其Transfer Function与meet/join操作都会有所不同，在迭代算法中，迭代求解器需要analysis的接口进行迭代操作。

框架概览

（三）算法实现

算法理论部分如下

活跃变量迭代算法

1、Transfer function

在活跃变量分析中，逻辑为反向的，举例而言，对于一个基本块BasicBlock，或者一个三地址表达式Statement，在其OUT中出现的变量，说明在这个基本块之后，执行结束（或者被redefine）之前，存在过use。而如果这些变量在该表达式中被定义，说明OUT之后的”use”承载的对象是刚刚赋值的。
所以有：$IN=OUT-def$
但是如果在该块中def之前被使用过，那么在该块IN的位置依然还是活跃的。
所以有：$IN=use\cup(OUT-def)$

public boolean transferNode(Stmt stmt, SetFact<Var> in, SetFact<Var> out) {
        // TODO - finish me
        SetFact<Var> OldIn=new SetFact<>();
        OldIn.set(in);
        in.union(out);
        if(stmt.getDef().isPresent()) {
            LValue lv=stmt.getDef().get();
            if(lv instanceof Var){
               in.remove((Var)lv);
            }
        }
        for(RValue rv:stmt.getUses()){
           if(rv instanceof Var){
               in.add((Var)rv);
           }
        }
        return (!in.equals(OldIn));
    }

2、meetInto

对于活跃变量分析而言，因为其需要遵循Soundness的要求，即某个Statement的OUT处只要有一条路径能够让这个变量“存活”即可，所以一个Statement的OUT集合为其后继所有可能存活的变量的并集。

public void meetInto(SetFact<Var> fact, SetFact<Var> target) {
        // TODO - finish me
        target.union(fact);
}

3、Solver

Solver实现的是迭代算法的最基本框架，在Solver中，遍历待分析程序的每一个基本块，对每一个基本块都进行meet+TransferFunction的操作，逐步迭代直至DataflowResult不发生改变为止。

protected void doSolveBackward(CFG<Node> cfg, DataflowResult<Node, Fact> result) {
        // TODO - finish me
        boolean IsChange=false;
        do{
            IsChange=false;
            for(Node node:cfg){
                if(!cfg.isExit((node))){
                    var succs=cfg.getSuccsOf(node);
                    for(Node succ:succs){
                        analysis.meetInto(result.getInFact(succ),result.getOutFact(node));
                    }
                    if(analysis.transferNode(node, result.getInFact(node), result.getOutFact(node))){
                        IsChange=true;
                    }
                }
            }
        }
        while(IsChange);
    }

4、Initialize

其实只有知道了上述的实现过程，才有可能在理论上知道如何初始化，在最开始时，DataflowResult应该有“不安全”的结果，即，每一个基本块在输入端都是不活跃的，因为Soundness的要求，我们只能要求找出最保险的结果，即所有变量活跃。

public SetFact<Var> newBoundaryFact(CFG<Stmt> cfg) {
    // TODO - finish me
    return new SetFact<>();
}
public SetFact<Var> newInitialFact() {
    // TODO - finish me
    return new SetFact<>();
}

Q&A

• Q：Transfer Function 是否在偏序集中单增？
  A：单增；
  证明：
  因为，IN=use并(OUT-def)，其中use和def由程序本身确定，且不会改变；
  所以，IN是否单增仅仅与OUT有关；
  因为，初始化阶段，所有的IN被设为空集，而所有的OUT又是IN的并集；
  所以，OUT最初的来源来自于各个基本块的use，而use中的元素是确定的，一旦进入集合，就无法被排除。
  因此，后期再次因为集合操作进入OUT的元素，其归根到底来源于use，也无法被排除到集合之外。
  综上，transferfunction单增。
• Q：该算法是否能够停止？
  A：能够停止；
  因为Transfer Function单增，而IN，OUT集合在偏序集中有上界（程序中定义的所有变量都活跃），所以一定存在不动点使f(IN)=IN，IN/OUT没有变化，算法停止。
• Q：初始化阶段为何为空？
  A：对于该问题，安全状态为“这个变量当前所储存的值在之后都可能被用到”（保证了所有变量值的可用），不安全状态为“这个变量当前所储存的值在之后没有可能被用到”，安全状态是确定的但是也是无用的，我们需要知道哪些变量的值之后都不可能用到了，所以只有从全部为空（不安全状态）开始，进行算法，算法停止时达到的不动点由于满足Transfer Function的设计而是安全的，且可以证明，该不动点为格上的最小不动点。
• Q：遍历顺序是否有关？
  A：无关，遍历顺序只是改变了每一个格中元素向格上不动点前进的路径，达到的不动点本身都是一样的。

Reference

基于南京大学软件分析课程的静态分析基础教程 https://static-analysis.cuijiacai.com/
”太阿“软件分析框架：https://tai-e.pascal-lab.net/
软件分析-南京大学：https://www.bilibili.com/video/BV1b7411K7P4/